Counting Sort (detailed pseudocode)
Verbose Pseudocode

#include <iomanip>
#include <iostream>
#include <sstream>
#include <algorithm>
#include <iterator>
#include <vector>
#include <string>
#include <cassert>
#define OUTPUT_ORDER
#define OUTPUT_EQUIVALENCE_CLASS
#define OUTPUT_START
#define OUTPUT_NEW_ORDER
#define OUTPUT_NEW_EQUIVALENCE_CLASS
using namespace std;
using Collection = vector< int >;
using Count = Collection;
using EquivalenceClass = Collection;
using Order = Collection;
using Start = Collection;
int main() {
/*
* class character
* ----- ---------
* 0 $
* 1 a
* 2 b
*/
const string S{ "ababaa$" }; const auto N = static_cast< int >( S.size() ), L = 1;
// ^^^^^^^ ----> a b a b a a $
// EquivalenceClass eClass{ 1,2,1,2,1,1,0 }; // commented out because this is derived below w/ counting sort
/*
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
*
* IMPORTANT NOTE: in this example 'order' is the count sort of single characters of the original string S,
* DO NOT confuse this with the suffix array 'order', which is different!
*
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
*
* recall: suffix array 'order' == begin index of the ordered suffixes of the original string S
*
* order suffix
* ----- ------
* 6 $
* 5 a$
* 4 aa$
* 2 abaa$
* 0 ababaa$
* 3 baa$
* 1 babaa$
*
* Order order{ 6,5,4,2,0,3,1 }; // <-- suffix array 'order' ( this is NOT used in this example !!! )
* $ a a a a b b
* $ a b b a a
* $ a a a b
* a b $ a
* $ a a
* a $
* $
*/
Initialization Phase


Order order( N ); { // the order of single characters of the original string S
/*
* compute a histogram of the number of times each key occurs within the original string S
*/
Count count( 123, 0 ); // 123 == 'z' + 1 ( +1 for 'a' through 'z' inclusive -- this was an arbitrary choice for the alphabet )
for( auto i{ 0 }; i < N; ++i ){
auto ch = S[ i ];
count[ ch ] = count[ ch ] + 1;
}
/*
* count[ '$' ] = 1
* count[ 'a' ] = 4
* count[ 'b' ] = 2
*/
/*
* prefix sum computation on count to determine, for each key,
* the position range where the items having that key should be placed in;
* i.e. items of key i should be placed in the range of [ count{ i-1 } : count{ i } )
* i.e. the range exists from count[ i-1 ] inclusive to count[ i ] non-inclusive ( one-past the actual range )
*/
for( auto j{ 1 }; j < 123; ++j )
count[ j ] = count[ j ] + count[ j-1 ]; // offset current count relative to previous count's offset
/*
* count[ '$' ] = 1 <-- count[ '$' ] = 1 offset by 0
* count[ 'a' ] = 5 <-- count[ 'a' ] = 4 offset by 1
* count[ 'b' ] = 7 <-- count[ 'b' ] = 2 offset by 5
*/
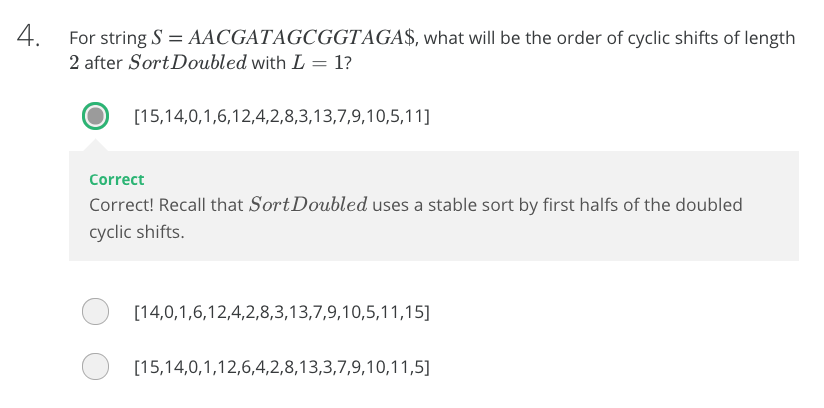
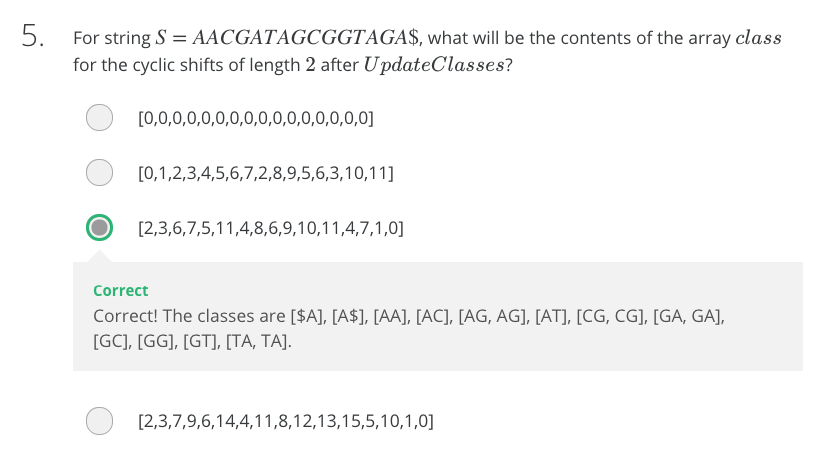
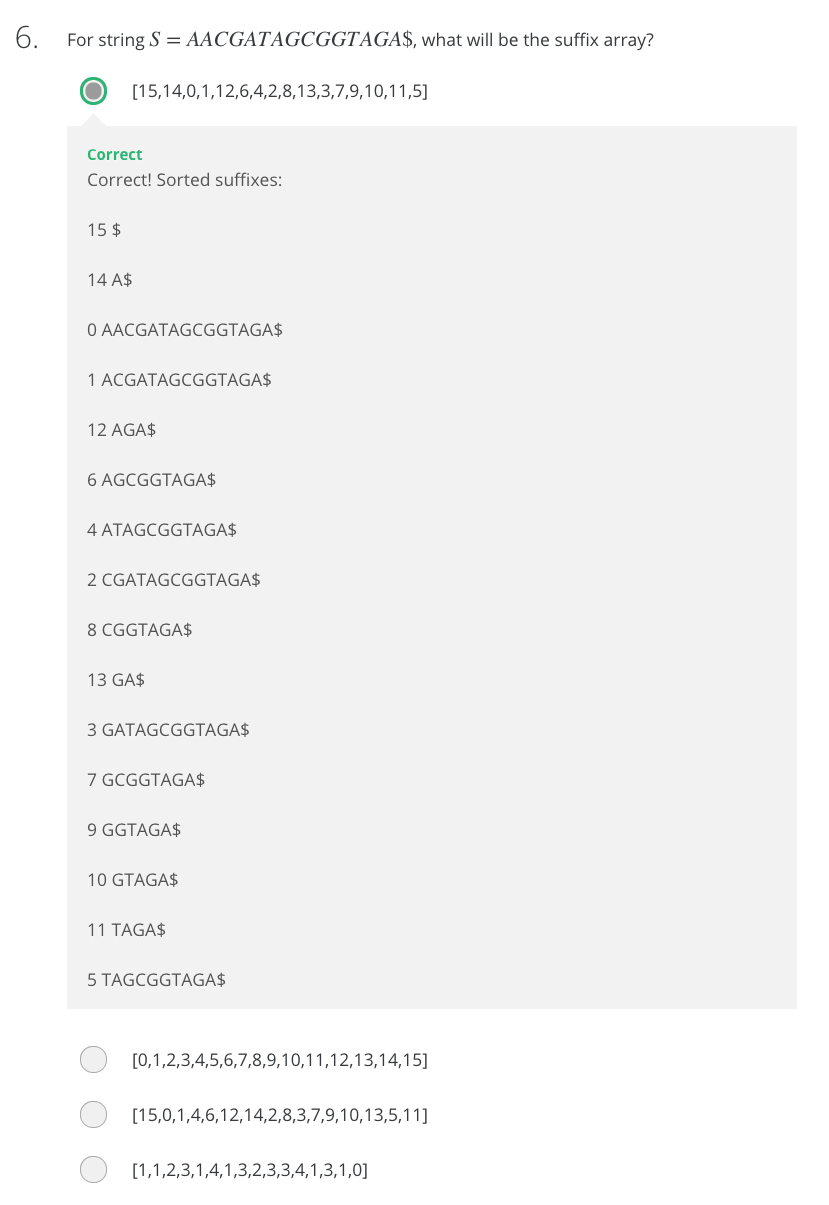
Quiz Question


Quiz Answer

/*
* move each (i)ndex into its sorted position
* NOTE: count[ ch ] is originally non-inclusive of the range (i)ndex will be placed witihin
* ( i.e. the value of count[ ch ] is one-past the actual range )
* that is why count[ ch ] is decremented before the (i)ndex is placed into that corresponding position
*/
for( auto i{ N-1 }; 0 <= i; --i ){
auto ch = S[ i ];
count[ ch ] = count[ ch ] - 1;
order[ count[ ch ] ] = i;
}
}
string order_str; {
ostringstream os;
os << "Order: "; copy( order.begin(), order.end(), ostream_iterator< int >( os, " " ) ); os << endl;
order_str = os.str();
assert( order_str == "Order: 6 0 2 4 5 1 3 \n" );
#ifdef OUTPUT_ORDER
cout << order_str << endl;
#endif
}



EquivalenceClass eClass( N ); {
eClass[ order[ 0 ] ] = 0; // '$' is always order[ 0 ], thus eClass[ '$' ] = 0 as the base case of the recurrence formula
for( auto i{ 1 }; i < N; ++i )
if( S[ order[ i ] ] != S[ order[ i-1 ] ] )
eClass[ order[ i ] ] = eClass[ order[ i-1 ] ] + 1; // diff equivalence class
else
eClass[ order[ i ] ] = eClass[ order[ i-1 ] ]; // same equivalence class
}
string eClass_str; {
ostringstream os;
os << "Class: "; copy( eClass.begin(), eClass.end(), ostream_iterator< int >( os, " " ) ); os << endl;
eClass_str = os.str();
assert( eClass_str == "Class: 1 2 1 2 1 1 0 \n" );
#ifdef OUTPUT_EQUIVALENCE_CLASS
cout << eClass_str << endl;
#endif
}
Transition Phase
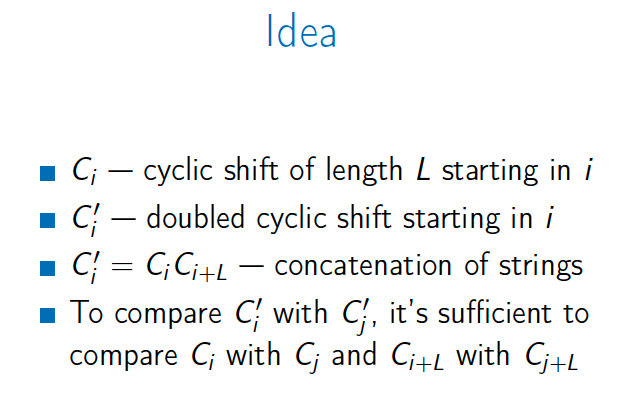
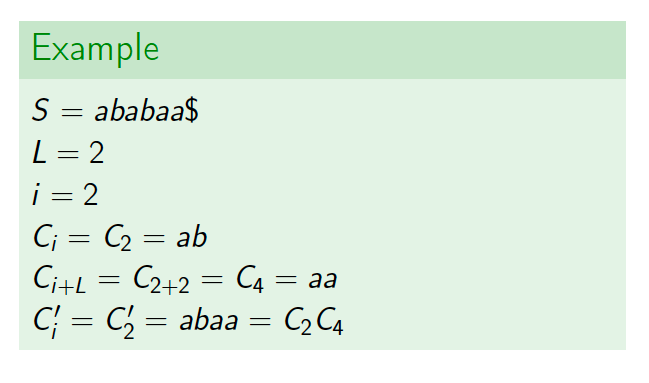




Count count( 123, 0 ); {
for( auto i{ 0 }; i < N; ++i ){
auto cl = eClass[ i ];
count[ cl ] = count[ cl ] + 1;
}
for( auto j{ 1 }; j < 123; ++j )
count[ j ] = count[ j ] + count[ j-1 ];
}
Start start( N ); {
for( auto i{ N-1 }; 0 <= i; --i )
start[ i ] = ( order[ i ] - L + N ) % N;
}
string start_str; {
ostringstream os;
os << "Start: "; copy( start.begin(), start.end(), ostream_iterator< int >( os , " " ) ); os << endl;
start_str = os.str();
assert( start_str == "Start: 5 6 1 3 4 0 2 \n" );
#ifdef OUTPUT_START
cout << start_str << endl;
#endif
}
Order new_order( N ); {
for( auto i{ N-1 }; 0 <= i; --i ){
auto cl = eClass[ start[ i ] ];
count[ cl ] = count[ cl ] - 1;
new_order[ count[ cl ] ] = start[ i ];
}
}
string new_order_str; {
ostringstream os;
os << "New order: "; copy( new_order.begin(), new_order.end(), ostream_iterator< int >( os, " " ) ); os << endl;
new_order_str = os.str();
assert( new_order_str == "New order: 6 5 4 0 2 1 3 \n" );
#ifdef OUTPUT_NEW_ORDER
cout << new_order_str << endl;
#endif
}
EquivalenceClass new_eClass( N ); {
new_eClass[ new_order[ 0 ] ] = 0; // "$..." is always order[ 0 ], thus eClass[ "$..." ] = 0 as the base case of the recurrence formula
for( auto i{ 1 }; i < N; ++i ){
auto pre = new_order[ i-1 ], preMid = ( pre + L ) % N,
cur = new_order[ i ], curMid = ( cur + L ) % N;
if( eClass[ pre ] != eClass[ cur ] || eClass[ preMid ] != eClass[ curMid ] )
new_eClass[ cur ] = new_eClass[ pre ] + 1;
else
new_eClass[ cur ] = new_eClass[ pre ];
}
}
string new_eClass_str; {
ostringstream os;
os << "New class: "; copy( new_eClass.begin(), new_eClass.end(), ostream_iterator< int >( os, " " ) ); os << endl;
new_eClass_str = os.str();
assert( new_eClass_str == "New class: 3 4 3 4 2 1 0 \n" );
}
#ifdef OUTPUT_NEW_EQUIVALENCE_CLASS
cout << new_eClass_str << endl;
#endif
return 0;
}
Quiz